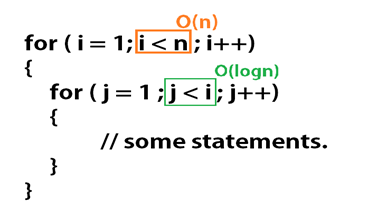Algorithm Analysis
Edited by TheGuyLoveNY, Jen Moreau
Algorithm Analysis:
Time Complexity: Time complexity also known as "Running Time" is a tool to measure the performance of the algorithm. Time complexity tells us how much time an Algorithm takes to run. There are 3 techniques that are used to find Time complexity of an algorithm.
- Big "O": Big O is specifically used to describe worst case scenario of an algorithm. It indicated the maximum time an algorithm will take to execute.
O(1) Indicated that the program will run at a constant speed regardless of the input size. For example : x+y=z; >> O(1) means Constant.
- Big "": Big indicated the minimum time an algorithm takes to executed with a given number of input size. Asymptotically Big represents Lower Bound.
- Big "": Big represents Tight bound, Asymptotically. It indicated the average time taken by an algorithm to execute for a given input size.
Examples:
Let's consider an example to understand Time complexity of Big "O":
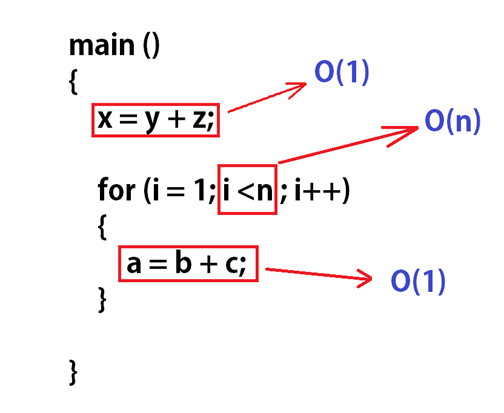
A sample program :
As you can see from the example, the Assignment and arithmetic operations are considered constant thus are represented with O(1). Secondly, In the loop where it's "I<n", Here the variable "I" is dependent on the input variable "n". So the larger the input size n is the longer the program will run hence it is not constant i.e O(n).
Now, Let us calculate the time complexity of the above program:
Big "O": O(1) + O(n)
= O( 1 + n)
Thus by ignoring the constant O(1), We can write:
= O(n)
Hence the Time complexity is O(n). Let's take another example to understand Time complexity better:
We can conclude that there is two Loop, Both, the Inner loop and the outer loop are dependent on the input size 'n'. So we have two O(n) and two constant O(1).
Here is how to calculate the time complexity:
Big "O": ( O(1) + O(n) + O(n) )
= O ( 1+ n + n)
Ignoring the constant O(1), we get:
= O ( n2)
Hence, the time complexity of the above program is O ( n2).
It is important to remember, That in nested loops , Outer loop will represent O(n) if it depends on the input size. Whereas, the inner loop will represent O(logn) if it depends on twice the input size or half of the input size.
Complexity Analysis:
Complexity analysis is the analysis of algorithm that determines how much amount of resources are needed. These resources can be time: the number of milliseconds a program takes to execute, or the the resources can be memory, i.e number of bytes the program takes to run.
Analysis of algorithm:
- Simple statements : These are the statements that take constant time to execute. The time complexity for simple statements: s1, S2, S3, … , sk, is O(1), which is constant. These statements are constant as long as the number of statements(k) is constant, meaning the number of statements don't change at run time, which is very likely.
- Loops : Loop statements are not constant and thus Its complexity is not constant as well. The loop's time complexity depends on the numbers of time the loop will iterate.
For example:
for( I = 0; I < n ; I++) { //something. }
Here, The loop's index variable "I" is dependent on the input variable "n", Hence the time complexity of this loop is O(n).
- Nested Loops: Nested loop refers to Loop inside another loop. This often gets confusing due to the fact that the inner loop will execute exponentially, depending on the outer loop.
Because of this, the time complexity will greatly vary For example:
for( I = 0; I < n ; I ++) { for( j = 0 ; j < I; j++) { //Inner loop statement. } }
Here, The Outer loop runs "n" times since it's dependent on the nth value. Whereas, the inner loop depends on the outer loop and that's where it executes exponentially. So, the time complexity of this Nested loop will be O(n2).
- Lower order terms: While finding time complexity, we should always ignore lower order term. Now, What is lower order term? You may ask. Well, Constant expression or simple statements gives O(1), which has lower preference over O(n), which has higher priority over constant O(1). Hence, O(1) is the lower order term in this case.
For example:
Time complexity : O(1) + O(1) + O(n)
Here, we have two lower order terms, i.e O(1). Hence, we ignore them. So, the final answer :
Time Complexity : O(n)
Another case: Similarly, Consider this next case.
Time Complexity : O(1) + O(n) + O(n2) Here, Again, the lower order term is O(1). So we remove O(1) out of the equation.
Now, Time Complexity : O(n) + O(n2)
If we look closely, we can figure out that O(n) is a lower order term and can be removed. Finally, Time Complexity : O(n2)
Asymptotic Complexity:
As discussed, we should concentrate on the higher term and should remove the lower term out of the equation. Similarly, for Asymptotic complexity, we only focus on higher value of n and ignore the rest of the term. It is important to remember, There can be only one term left to define the complexity, That is why we keep removing the lower order term until the highest order term is left.
Here is the Asymptotic complexity for all the sort we have come across so far.
- Merge sort : Best case.
- Insertion sort : Average case.
- Selection sort : Worst case.
This article is part of a series on 'Design and Algorithm Analysis'. Read the full series here:
1) Design and Algorithm Analysis Overview
2) Algorithm_Analysis
4) Algorithm Graph in Data Structure
5) Types and Styles of Algorithm Searchs
7) Design and Algorythm of Dynamic Programming
Referencing this Article
If you need to reference this article in your work, you can copy-paste the following depending on your required format:
APA (American Psychological Association)
Algorithm Analysis. (2017). In ScienceAid. Retrieved Apr 19, 2024, from https://scienceaid.net/Algorithm_Analysis
MLA (Modern Language Association) "Algorithm Analysis." ScienceAid, scienceaid.net/Algorithm_Analysis Accessed 19 Apr 2024.
Chicago / Turabian ScienceAid.net. "Algorithm Analysis." Accessed Apr 19, 2024. https://scienceaid.net/Algorithm_Analysis.
If you have problems with any of the steps in this article, please ask a question for more help, or post in the comments section below.
Comments
Article Info
Categories : Design and Algorithm Analysis
Recent edits by: TheGuyLoveNY