Algorithm Graph in Data Structure

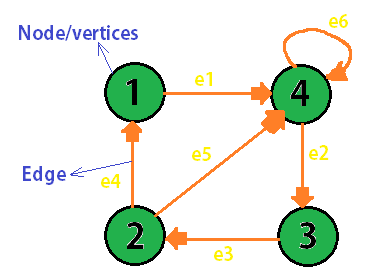
A graph is an abstract data type that is used to represent Direct and indirect graphs. A graph contains set of vertices also called points or nodes and a set of edges also called arcs or lines. Here is a look at a simple Graph with 4 Nodes/vertices and 5 Edges/Lines.

Vertices : { 1, 2, 3, 4 } Edges : { e1, e2, e3, e4, e5, e6 } Isomorphic Graph: Isomorphic Graph is a directed graph. This type of graph contains at least one vertex or node that is not connected to any node not even to itself. This graph does not connect the node completely since there is at least one node which not connected.

Example of Isomorphic Graph:

Edges :

So far we came across two different graphs, the First graph had lines with names e1, e2 and so on. The latter, however, does not have any names on its edge. This is because there are two types of edges.

1. 1
   Weighted Edge.

   Advertisement

   Was this step helpful? Yes | No| I need help
2. 2
   Non-weighted Edge.

   Was this step helpful? Yes | No| I need help

Weighted edge is the one given weightage such as a number: 1, 2, 3, etc. Non-weighted edge does not have any weightage but is given any name to identify that edge such as e1, e2, and so on. This weightage are used to find out which path is expensive and which is inexpensive. The graph is weighted by summing all the weighted edges. So to find the total weight of any graph we use this formula:

Total weight = Sum of all weights in the graph.

Adjacency Matrix:

The adjacency matrix is used to indicate if the graph has an adjacent pair or not. Adjacency matrix uses a square matrix to represent a finite set of the graph. The adjacency matrix is used (0,1) matrix to represent edges on a graph.

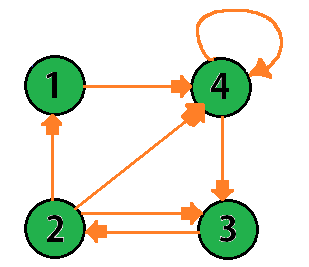
Graph G1:

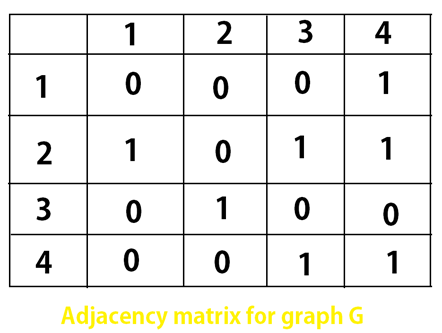
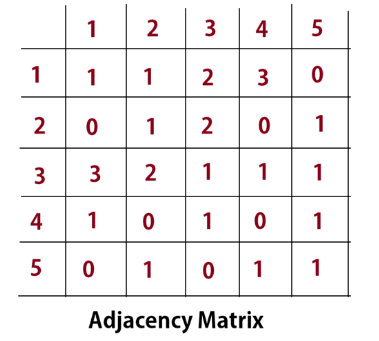
Adjacency Matrix for Graph G1:

As you can see the adjacency matrix uses 1s and 0s to represent the connection between nodes. Here 1 means connected and 0 means disconnected. Adjacency matrix searches for a number of edges a graph has. As shown in the picture above, 4 represents the node no.4 and 1 represents it's connection to other nodes. As Row 4 has two 1s, one in column 3 and other in column 4. This means the node 4 is connected to node 3 and Node 4 (self).

Example: Find Adjacency matrix of Graph G2.

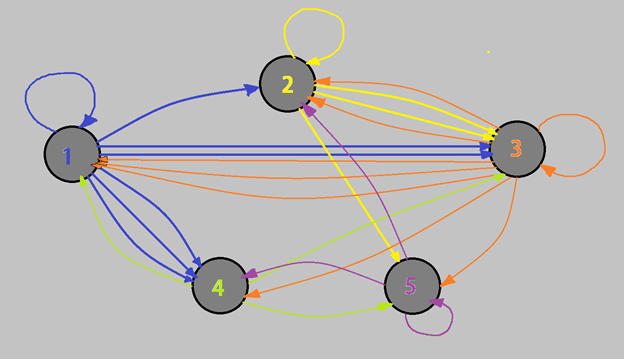
Graph G2:

As we see that each number of lines connected to a node is represented in the adjacency matrix. For example, Node 1 is connected to node 4 with 3 lines. Hence, the adjacency of node 1 to node 4 is 3.

1) Design and Algorithm Analysis Overview

2) Algorithm Analysis

3) Algorithm Sorting

4) Algorithm_Graph

5) Types and Styles of Algorithm Searchs

6) Types of Algorithm Laws

7) Design and Algorythm of Dynamic Programming

If you need to reference this article in your work, you can copy-paste the following depending on your required format:

APA (American Psychological Association)
Algorithm Graph in Data Structure. (2017). In ScienceAid. Retrieved Apr 19, 2024, from https://scienceaid.net/Algorithm_Graph

MLA (Modern Language Association) "Algorithm Graph in Data Structure." ScienceAid, scienceaid.net/Algorithm_Graph Accessed 19 Apr 2024.

Chicago / Turabian ScienceAid.net. "Algorithm Graph in Data Structure." Accessed Apr 19, 2024. https://scienceaid.net/Algorithm_Graph.

If you have problems with any of the steps in this article, please ask a question for more help, or post in the comments section below.

Comments