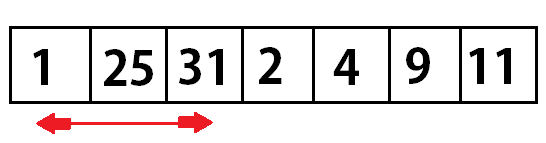Algorithm Sorting
Edited by TheGuyLoveNY, Jen Moreau
Algorithm Sorting:
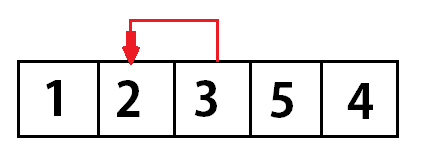
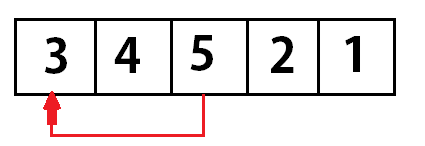
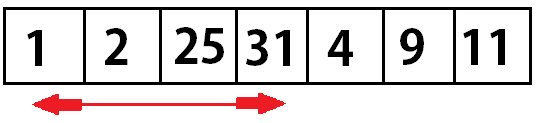
Selection sort: Selection sort is one of the simple sorting algorithms. In selection sort algorithm, The list or array is divided into two lists. The algorithm stores all the sort numbers in one list and all the other unsorted numbers in other list. This algorithm is the simplest but performs the worst when the array size is large. Hence, It is useful for smaller array size.
Passes are nothing but a number of steps required to solve the problem. A number of passes: n(n-1), where n is the number of input size. So if there are 3 numbers in a list then the selection sort will take 6 steps to sort the numbers.
Example :
An array of 5 numbers.
- Search the smallest and swap with Index 1.
- Again, Search the smallest and swap.
- Repeat the process until all the numbers are sorted.
Insertion sort:
Insertion sort is another simple sorting algorithm that is used to sort an average number of the list. Insertion sort is better than selection sort but worse than other sorting algorithms such as quicksort, heapsort, mergesort. Insertion sort also has a same number of passes as selection sort, i.e n(n-1). Insertion sort works by sorting all the numbers in one final sorted list or array, one at a time.
Worst Case: О(n2) Best Case: O(n) Average Case: О(n2)
Example :
Sorting the list of 5 numbers using Insertion sort.
Step 1 :
Step 2:
Step 3:
Step 4:
For example: Sort Using Insertion sort.
- Step 1:
- Step 2:
- Step 3:
- Step 4:
- Step 5:
- Step 6:
Total Passes: 6
Merge Sort:
Merge sort is one of the most efficient sorting algorithms. It's better than Selection sort and Insertion sort that we have studied so far. Merge sort is far better because of the fact that it uses "Divide and Conquer" approach. Basically, Merge sort take a list of numbers and divide them into two sublists and solve them. Much like Divide and conquer, It divides the number list into sublist and conquers, i.e sort that sublist and merge them back to a single Sorted list.
Merge sort Performance:
- Worst-case Performance : O(n log n)
- Average-case performance : O(n logn)
- Best-case performance : O(n)
Algorithm:
- 1If there is only one element then it is sorted already, Return.Advertisement
- 2Divide the list into two halves until the list can no longer be divided.
- 3Sort all the sublists and then merge them into a single sorted list.
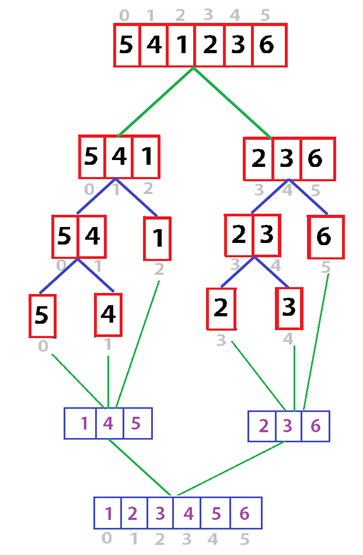
Here is a depiction of merge sort for a much better understanding:
Figure 13.0
Example: Sort the following list of numbers using Merge sort.
Figure 14.0
Solution: Merge sort uses Divide-Conquer method to sort numbers of a list.
Figure 14.1 Example 2: Sort the list of numbers using Merge sort algorithm.
Figure 15.0
Solution: Using Merge sort algorithm the solution is as follows:
Figure 15.1
Radix Sort:
Radix sort is a sorting algorithm but very different in terms of its approach. Radix sort is a different sorting algorithm compare to all the sorting algorithm we came across so far. Radix sort uses non-comparative integer technique. It sorts numbers in terms of the keys. It basically breaks all the numbers digits and store them according to their keys. We sort numbers from LSB, i.e Least Significant Bits to MSB or Most Significant Bits.
Radix sort performance :
- Worst-Case performance : O(wn)
- Worst-Case Space complexity : O(w + N)
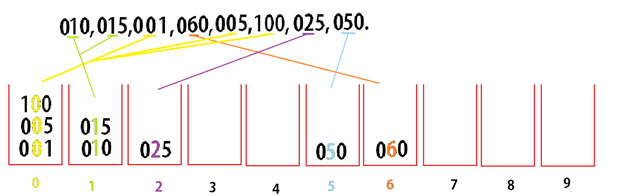
Let's take an example: Sort the following numbers using Radix sort.
Numbers : 10, 15, 1, 60, 5, 100, 25, 50.
Solution:
Figure 16.1 : Pass 1
In Pass 1, Radix sort compares digits of the numbers that are to be sort. The algorithm then push those number according to their last digits, In the above case, All the numbers that ends with 0s are all pushed in the "Bucket 0". We also balance all the numbers with same number of digits.
Pass 2:
Figure 16.2 : Pass 2.
In pass 2, The algorithm compares all the second digit of the numbers and put them into the bucket according to those numbers. Let's pick 0, In the bucket 0, All the numbers with last second digit as 0s are thrown in the bucket 0. Also, Notice that the algorithm has now added extra 0 at the start of every number, This is to balance the number of digit, since there is a number 100 in the list with 3 digit.
Pass 3:
Figure 16.3: Pass 3.
In Pass 3, All the first digit of the numbers are compared and stored in the bucket accordingly. Since all the elements in the list are added with 0 at the start since they all were smaller than 100. All those numbers are in Bucket 0 and only 100 in Bucket 1.
Finally, All the numbers are then taken out of the bucket sequentially. And we get a list of sorted number. This is how radix sort works.
Sorted List : 001, 005, 010, 025, 050, 060, 100.
Counting Sort :
Counting sort is an integer sorting algorithm used to sort numbers on the basis of counting number of distinct values and performing arithmetic operation to locate the position. In other words, the algorithm uses numeric keys to sort the given numbers of list. This algorithm is often used in subroutine algorithm. It is good to note that this sort does not perform any comparison on the numbers.
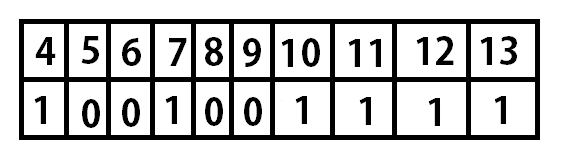
For example: Use counting sort algorithm to sort the following list of numbers.
Figure 17.1
Solution : Here, We will first find the lowest value, i.e 4 and the greatest value, i.e 13. So, Minimum value : 4 Maximum value : 13
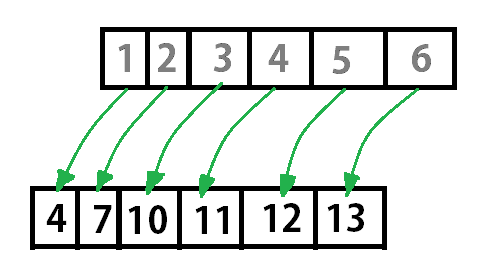
Now, Create index from minimum to maximum value.
Figure 17.2
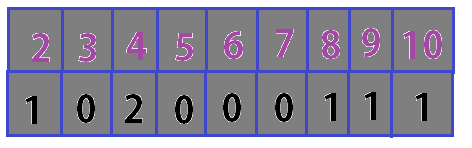
Then, create occurrence table (Figure 17.3)
Figure 17.3
Now Count the numbers in the array (Figure 17.3). Minimum count = 1 Maximum count = 6
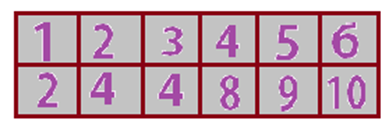
Since, the Minimum count is 1 and the maximum count is 6. We can assume that the array is of index 6. We, Therefore, Assign the index to the respective numbers (Figure 17.4).
Figure 17.4
Hence, The final sorted list after the process: Figure 17.5
Figure 17.5 : Sorted list.
Example 2:
Sort the following numbers of list using Counting sort Algorithm.
Figure 18.0
Now, We first find out the smallest and the greatest numbers in the list.
Minimum Value : 2 Maximum Value : 10
Now, Create Index table : Figure 18.1
Figure 18.1
Create occurrence table : Figure 18.2
Figure 18.2
Sum count : Figure 18.3
Figure 18.3
Sum count : Figure 18.4
Figure 18.4
Hence, we have sorted the list using Counting sort algorithm.
Bucket Sort:
Bucket sort is another sorting algorithm which uses buckets for sorting numbers in a list. Bucket sort is quite similar Radix sort due to the fact that bucket sort algorithm uses buckets to sort. Bucket sort also known as bin sort, Uses different approach to sort the numbers, once stored in bucket. Basically, Bucket sort start processing by first categorizing numbers then storing them in buckets. Once the numbers are stored in the buckets, It either uses different sorting algorithms to sort these numbers or recursively keep categorizing the numbers in buckets until no categorization is possible.
Performance :
Performance wise Bucket sort is the least efficient algorithm compared to other sorting algorithms like Insertion sort, merge sort or bubble sort.
Here is the time complexity of bucket sort algorithm:
- Worst case performance : O(n2)
- Average case performance : (n + k)
- Best case performance : (n + k)
- Worst case Space complexity : O(n.k)
Now, Let us take some examples to understand bucket sort algorithm.
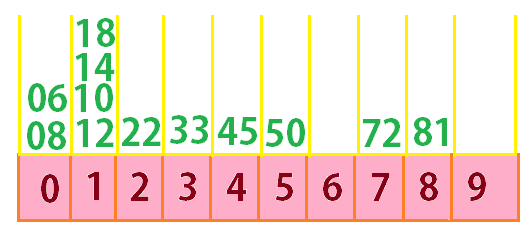
For example: Use Bucket list algorithm to sort the following numbers of list.
Solution:
We start off by calculating, Minimum and maximum values in the list.
Minimum value = 6 Maximum value = 81 Total numbers = 12
Divider = 10 ( Unit place, always 0-9) Categorize numbers into buckets:
Formulae :
Divider = Ceil ( Max + 1 )Divider
Now, We use the formulae above to calculate divider.
- Ceil ( 81 + 1 )10 = ( 82 )10 = 8.2
- Ceil ( 2 + 1 )10 = ( 23 )10 = 2.3
- Ceil ( 45 + 1 )10 = ( 46 )10 = 4.6
- Ceil ( 12 + 1 )10 = ( 13 )10 = 1.3
- Ceil ( 8 + 1 )10 = ( 9 )10 = 0.9
- Ceil ( 10 + 1 )10 = ( 11 )10 = 1.1
- Ceil ( 6 + 1 )10 = ( 7 )10 = 0.7
- Ceil ( 72 + 1 )10 = ( 73 )10 = 7.3
- Ceil ( 33 + 1 )10 = ( 34 )10 = 3.4
- Ceil ( 18 + 1 )10 = ( 19 )10 = 1.9
- Ceil ( 50 + 1 )10 = ( 51 )10 = 5.1
- Ceil ( 14 + 1 )10 = ( 15 )10 = 1.5
Finally, The numbers are sorted based on the values calculated above:
This article is part of a series on 'Design and Algorithm Analysis'. Read the full series here:
1) Design and Algorithm Analysis Overview
3) Algorithm_Sorting
4) Algorithm Graph in Data Structure
5) Types and Styles of Algorithm Searchs
7) Design and Algorythm of Dynamic Programming
Referencing this Article
If you need to reference this article in your work, you can copy-paste the following depending on your required format:
APA (American Psychological Association)
Algorithm Sorting. (2017). In ScienceAid. Retrieved Apr 19, 2024, from https://scienceaid.net/Algorithm_Sorting
MLA (Modern Language Association) "Algorithm Sorting." ScienceAid, scienceaid.net/Algorithm_Sorting Accessed 19 Apr 2024.
Chicago / Turabian ScienceAid.net. "Algorithm Sorting." Accessed Apr 19, 2024. https://scienceaid.net/Algorithm_Sorting.
If you have problems with any of the steps in this article, please ask a question for more help, or post in the comments section below.
Comments
Article Info
Categories : Design and Algorithm Analysis
Recent edits by: TheGuyLoveNY