Design and Algorythm of Dynamic Programming

Dynamic programming is an approach to solving problems, In which problems are broken into smaller problems, i.e subproblems. Much like Divide and conquer approach but In dynamic programming, Not only we divide the problem into a smaller set and solve those subproblems but we also store the result of these different subproblems. So whenever in future we do not have to recompute the same problem, Instead just retrieve back previously solved problems (which are stored in memory data structures). Dynamic programming is often used for optimization. Since dynamic programming keeps track of all the previously encountered problems and figures out the optimal (efficient) solution.

There is two main aspect for a problem to be solved by dynamic programming:

1. 1
   Optimal structures.

   Advertisement

   Was this step helpful? Yes | No| I need help
2. 2
   Overlapping-subproblems.

   Was this step helpful? Yes | No| I need help

If a problem can be solved by breaking it into subproblems and then merging them to a single piece of the solution then such problem is referred as optimal structures. Merge sort and Quicksort follows this approach and hence are not considered as dynamic programming.

Overlapping-subproblems refers to the small subproblems that can be recursively solved and will not generate any new problem. Algorithms like Bellman-Ford, Floyd-Warshall falls under this category.

Techniques that are used in dynamic programming are mainly:

• Tabulation.
• Memorization.

Dynamic programming can be achieved using two ways:

1. 1
   Bottom-Up approach.

   Was this step helpful? Yes | No| I need help
2. 2
   Top-Down approach.

   Was this step helpful? Yes | No| I need help

Hashing is the process of searching a variable from computer memory. Hashing searches for the key stored in a hash table with the help a hash function. Hashing is one of the fastest searching techniques. Hashing uses the most basic Binary search.

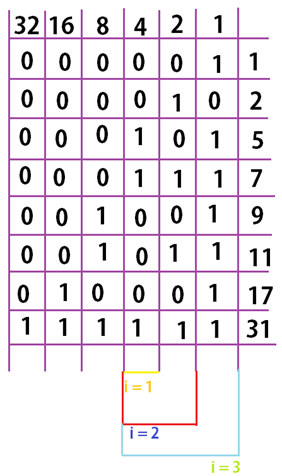
Here is a quick example:

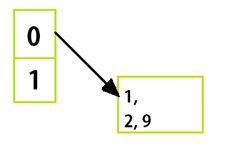
First, put them on the hash table according to their values:

Level 1:

Check whether any number in the list ends with digit 0 (none in our case).

For example :

Then check for the numbers that end with 1.

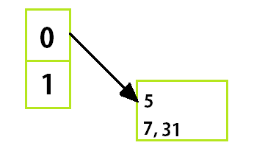
Level 2:

There is no buffer overflow. Hence, We can stop hashing. If there would have been any buffer overflow, we would have proceeded to next level, i.e Level 3.

1) Design and Algorithm Analysis Overview

2) Algorithm Analysis

3) Algorithm Sorting

4) Algorithm Graph in Data Structure

5) Types and Styles of Algorithm Searchs

6) Types of Algorithm Laws

7) Dynamic_Programming

If you need to reference this article in your work, you can copy-paste the following depending on your required format:

APA (American Psychological Association)
Design and Algorythm of Dynamic Programming. (2017). In ScienceAid. Retrieved Jun 3, 2023, from https://scienceaid.net/Dynamic_Programming

MLA (Modern Language Association) "Design and Algorythm of Dynamic Programming." ScienceAid, scienceaid.net/Dynamic_Programming Accessed 3 Jun 2023.

Chicago / Turabian ScienceAid.net. "Design and Algorythm of Dynamic Programming." Accessed Jun 3, 2023. https://scienceaid.net/Dynamic_Programming.

If you have problems with any of the steps in this article, please ask a question for more help, or post in the comments section below.

Comments