Gravitational Field

The Oxford English Dictionary defines a gravitational field as "the region of space surrounding a body in which another body experiences a force of gravitational attraction," ^[1]. When Sir Isaac Newton was hit on the head with an apple while sitting under a tree, he discovered a pull to the earth surface which he termed the gravitational force. This discovery led Newton's foundation studies into the force of attraction between two surfaces or masses in a gravitational field.

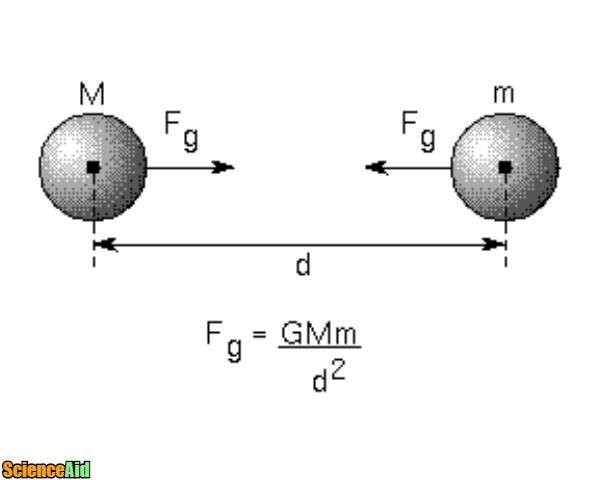
Newton proposed; "The force of attraction between two masses is directly proportional to the product of the masses."

                                           F∝M_1 M_2

"The force of attraction between these masses is inversely proportional to the square of their distance apart."

                                         F∝1/r^2 

The second equation is usually referred to as Inverse Square Law. The combination of the two expressions above demonstrates Newton's Universal Law of Gravity "The force of attraction is directly proportional to the product of the masses M1 and M2 and inversely proportional to the square of their distance apart."

                                      F∝(M_1 M_2)/r^2 

Mathematically,

                                   F∝(M_1 M_2)/r^2 

                                  F=(GM_1 M_2)/r^2 

Where M1= The first body (mass)

           M2= The second body (mass)
            r= Distance between the two bodies
           G= Gravitational constant which is 6.67x10-11 Nm-2/Kg2

The gravitational constant (G) is used in computing the force of attraction between any two masses. The acceleration due to gravity (g) is the acceleration near the surface of the earth due to the attraction between the mass of the earth and objects attracted to the earth that are close to the earth's surface.

In reality, the value of G is not constant across the surface of the earth. For example, the gravitational constant recorded in the polar regions is unarguably different to the gravitational constant close to the equator. Its value varies across the earth's surface. It is essential to discuss the relationship between the gravitational constant (G) and acceleration due to gravity (g) because it gives us the accurate value of one if the other is known at any location of the globe.

We can recall from the universal gravitational law;

                                             F=(GM_1 M_2)/r^2 

We can re-write the equation to give the expression of the gravitational force between the earth and an imaginary object with mass M, we have;

                                             F=(GM_E M)/〖r^2- _E 

Also, recall that,

                                             F=mg

Therefore,

                                         Mg=(GM_E M)/〖r^2- _E 

The mass (M) will cancel out each other, leaving us with the expression below;

                                          g=(GM_E)/〖r^2- _E 

Where ME= mass of earth

            G= Gravitational constant
            rE= radius of the earth

The gravitational potential energy between two objects of a particular mass is the potential for the objects to move caused by their gravitational attraction. This attraction turns the potential energy into the kinetic energy, and the objects will move toward each other.

Gravitational potential can be described as the work done in bringing a unit mass from infinity to the surface,

Mathematically,

                                           V=GM/r

Where V=Gravitational potential M= Mass r=Distance apart

Escape velocity is the velocity an object needs to be traveling in other to break free of a planet's gravity and leave it without further propulsion. Also, it is the velocity or speed required by an object to move away under the influence of gravity.

Recall;

                                          Energy=F  -  r

                                        Energy=(GM_E M)/〖r^2- _E   -  r_E   

                                          Energy=(GM_E M)/r_E 

Since it is a moving energy (Kinetic energy),

                                                     KE=(GM_E M)/r_E 

Since;

                                                    KE=1/2 Mv^2

We have;

                                                   1/2 Mv^2=(GM_E M)/r_E 

                                                    v^2=(2GM_E)/r_E 

Recall that, from the relationship between acceleration due to gravity and gravitational constant;

                                      g=(GM_E)/〖r^2 - _E  (Relationship between g and G)

                 M_E=(g〖r_E - ^2)/G  (substitute the value of ME into KE equation)

                                            v^2=(2G[(g〖r_E- ^2)/G])/r_E 

                                            v^2=2gr_E

                                           v=√(2gr_E )

Where v=velocity is required to leave the planet (escape velocity)

            rE=radius of the earth
            g= acceleration due to gravity

From the expression of the escape velocity above, we can compute the escape velocity of any planet. The escape velocity of the earth is 11313 ms-1 while the escape velocity of the moon is 2456ms-1. The bigger the planet, the higher the escape velocity.

If you need to reference this article in your work, you can copy-paste the following depending on your required format:

APA (American Psychological Association)
Gravitational Field. (2017). In ScienceAid. Retrieved Apr 19, 2024, from https://scienceaid.net/Gravitational_Field

MLA (Modern Language Association) "Gravitational Field." ScienceAid, scienceaid.net/Gravitational_Field Accessed 19 Apr 2024.

Chicago / Turabian ScienceAid.net. "Gravitational Field." Accessed Apr 19, 2024. https://scienceaid.net/Gravitational_Field.

If you have problems with any of the steps in this article, please ask a question for more help, or post in the comments section below.

Comments

1. ↑ https://en.oxforddictionaries.com/definition/gravitational_field