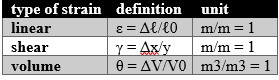Understand Elasticity

WHAT IS ELASTICITY:

Elasticity is the ability of a solid material to return to its original shape and size after the forces deforming it have been removed. From Hooke's law which states that the force required to restore a spring is directly proportional to the extension produced, provided elastic limit is not exceeded.

If we replace the word "extension" with the symbol (x), "force" with the symbol (F), and a constant of proportionality (k), then, to show that the stretched object was trying to return to its original state, we would add a negative sign (-). Therefore, we have F = -k X x Hooke's law was referring to spring, but to an imaginary object, Hooke's law can be generalized to Stress is proportional to strain. Where strain refers to a change in dimension (length, area, volume or angle) compared to its original value and stress refers to the force the caused the change. The coefficient that elasticity is referred to as elastic modulus.

Elastic modulus is the property of the material.

Table 1 Elastic Modulus for length, area, and volume.

The international standard symbols for the moduli are Y for Young's, S for shear, and B for bulk. Stress on a solid is described as a force divided by its area of contact.The SI unit of stress is the newton per square meter (N/m2) or Pascal (Pa) named in honor of Blaise Pascal (1623-1662) while strain is dimensionless. Recall that, strain can be a change in length, area or volume as shown in table 2. Which implies that Pascal is also the SI unit for all the three moduli

Table 2 Types of strain

YOUNG'S MODULUS

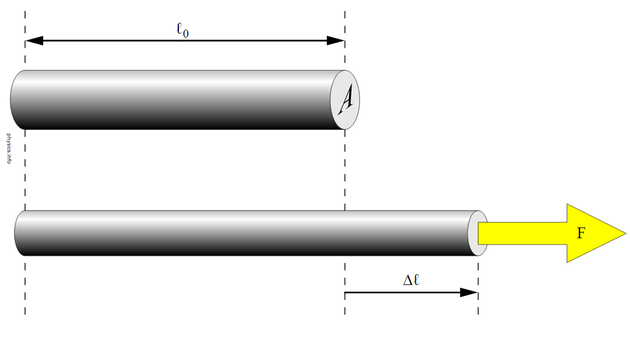
The quantity that describes a material's response to stresses applied normal to opposite faces is called Young's modulus in honor of the British scientist Thomas Young (1773-1829). The symbol for Young's modulus is usually Y. Young's modulus is defined for all shapes and sizes by the same rule, but for brevity, imagine a rod of length 0 and cross sectional area A being stretched by a force F to a new length 0 + .

Figure 1 Stretched Material Tensile stress is the outward normal force/area (σ = F/A) and tensile strain is the fractional increase in length of the rod (ε = /0). The proportionality constant that relates these two quantities together is the ratio of tensile stress to tensile strain Young's modulus.

F/A=E ∆l/l_o

σ=Yε

The same relation holds for forces in the opposite direction; that is, a strain that tries to shorten an object. The SI units of Young's modulus is the pascal (Pa) The direction of a linear stress is called the axial direction, that is stress can be compressive or contractive.

SHEAR MODULUS

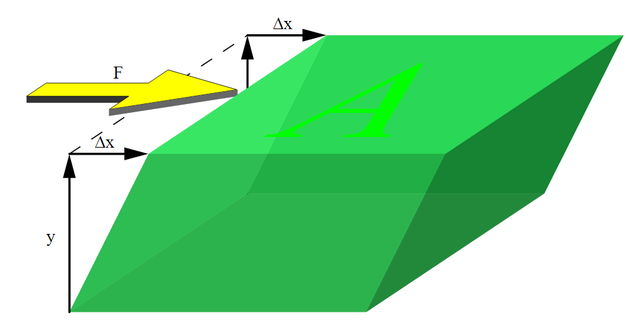
A force applied tangentially to the face of an object is called a shear stress. The deformation that occurs is called shear strain. Applying a shear stress to one face of a square box slides that face in a direction parallel to the opposite face and changes the adjacent faces from square to parallelograms.

Figure 2 Shear stress demonstration

The coefficient that relates shear stress (τ = F/A) to shear strain (γ = ∆x/y) is called the shear modulus (S). F/A=G ∆x/y τ=Gγ

Fluids (liquids, gasses) cannot resist a shear stress. They flow rather than deform. The quantity that describes how fluids flow in response to shear stresses is called viscosity and is beyond the scope of this topic.

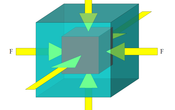
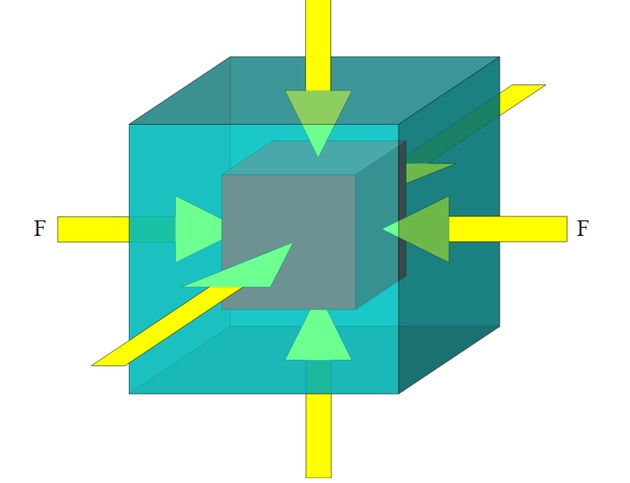
BULK MODULUS

A force applied uniformly over the surface of an object will compress it uniformly. This changes the volume of the object without changing its shape.

Figure 3: Bulk modulus

The stress, in this case, is simply described as a pressure (P = F/A). The resulting volume strain is measured by the small change in volume (θ = ∆V/V0). The coefficient that relates stress to strain under uniform compression is known as the bulk modulus or compression modulus (B).

F/A=K ∆v/v_o

P=Kθ

Gasses have a bulk modulus that varies with initial pressure, which makes it more of a subject for thermodynamics, especially gas laws. The reciprocal of bulk modulus is called compressibility (usually represented as β ). A material with a high compressibility experiences a large volume change when pressure is applied. β=1/K Therefore, the SI unit of compressibility is the inverse of pascal 〖Pa� - ^(-1).

If you need to reference this article in your work, you can copy-paste the following depending on your required format:

APA (American Psychological Association)
Understand Elasticity. (2017). In ScienceAid. Retrieved Apr 2, 2023, from https://scienceaid.net/Understand_Elasticity

MLA (Modern Language Association) "Understand Elasticity." ScienceAid, scienceaid.net/Understand_Elasticity Accessed 2 Apr 2023.

Chicago / Turabian ScienceAid.net. "Understand Elasticity." Accessed Apr 2, 2023. https://scienceaid.net/Understand_Elasticity.

If you have problems with any of the steps in this article, please ask a question for more help, or post in the comments section below.

Comments