Convex Mirrors

Also called diverging mirrors, are spherical mirrors having a polished outer surface.

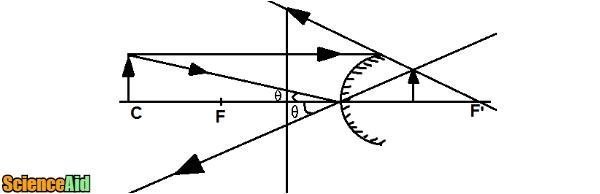
In the case of a convex mirror, the rays coming from an object do not meet or converge to a single point after reflection. Therefore an image is formed behind the mirror as shown in the figure by extending the reflected rays backward as dotted lines.

In the case of a convex mirror, only virtual images are produced. All these images are located between the pole of the mirror and the principal focus.

The images formed by convex mirrors are found to be:

• erect
• virtual
• smaller in size than the object. (Whether the object is located beyond C, on C, between F&C or any other point).

Spherical Mirror Formula:

The mathematical relationship between the object distance "p", image distance "q" and focal length "f" is given by the formula:

                                     1/f= 1/p+1/q

Where 'f' denotes focal length, 'p' denotes the distance of the object from the mirror and 'q' denotes the distance from the image to the mirror.

In order to derive the mirror formula, we use a ray diagram in which an object is placed between 'f' and 'c'. (Say)

The object is shown as OO' and image as II'. Consider two similar triangles OO'P and II'P

                               �"OO'P ß-----à II'P
            
                               m ∠1= m ∠2  and m ∠ 3=m ∠4  (Triangles are similar)
                                
                               OO' /II'= OP/I'P 
                        
                               OO'/II'= P/q --------------- (1)

Now

                               �"QPF ß-----à II'F 

                               (m ∠5= m ∠6  and  m ∠ 4=m ∠7 (Triangles similar)

In the figure; OP= p (object distance) I'P= q (image distance) PF= f (focal length)

                                QP/ II'=PF/I'F

                                OO'/II'=f/q-f ----------------- (2)
       

Now comparing (1) and (2)

                                p/q= f/q-f                   

                                p ( q-f) =qf

                                pq-pf= qf      

                                (Subtracting both sides by pqf)

                                1/f-1/q= 1/p

                                1/f= 1/p+1/q ------------------- (3) 

                                Eq (3) is the required mirror formula.

The size of the image depends on the position of the object from the mirror. The image may be greater, smaller or equal to the object size.

The ratio of the size of the image to the size of the object is called linear magnification and is denoted by 'M'.

                               M= hi/ho

                               hi= size of the image

                               ho= size of the object

'OR'

Magnification is also defined as the ratio of the distance of the image from the mirror to the distance of the object from the mirror itself, and is represented as;

                             M= q/p

                             Q= distance of image

                             P= distance of the object

Sign Conventions:

While applying the mirror formula or magnification formula or another relative case the following sign conventions are adapted to get better results in a given problem of image formation by a mirror.

1. 1
   All distances are measured from the pole of the mirror

   .

   Advertisement

   Was this step helpful? Yes | No| I need help
2. 2
   Distances of real objects and real images are taken as positive.

   Was this step helpful? Yes | No| I need help
3. 3
   Distances of virtual objects and virtual images are taken as negative

   .

   Was this step helpful? Yes | No| I need help
4. 4
   The focal length of a concave mirror is taken as positive and that of a convex is taken as negative.

   Was this step helpful? Yes | No| I need help

If you need to reference this article in your work, you can copy-paste the following depending on your required format:

APA (American Psychological Association)
Convex Mirrors. (2017). In ScienceAid. Retrieved Apr 26, 2024, from https://scienceaid.net/Convex_Mirrors

MLA (Modern Language Association) "Convex Mirrors." ScienceAid, scienceaid.net/Convex_Mirrors Accessed 26 Apr 2024.

Chicago / Turabian ScienceAid.net. "Convex Mirrors." Accessed Apr 26, 2024. https://scienceaid.net/Convex_Mirrors.

If you have problems with any of the steps in this article, please ask a question for more help, or post in the comments section below.

Comments