Types and Styles of Algorithm Searchs

Search Algorithms are one of the most important aspects of a computer. Every action involves some kind of searching my the computer. For example, If a user wants to open a file called "File1", Then the computer will first search for the file with name File1. If the file is found then it will open that file for the user or will report an error otherwise. Either Way, the computer is supposed to do these action faster. Today's computer uses best search algorithms to find files for the user. Even Google uses Bestest search algorithm as Google is a search engine, It's searching algorithm has to be the fastest possible. The better the search algorithm is the faster the computer will search a file for the user. There are many search algorithms available, but it ultimately comes down to what the goal is. Choosing a search algorithm depends on the type of application the programmer is developing.

Depth First Search (DFS):

Depth First Search is one of the searching algorithms that is used to search nodes in a tree or graph data structure. As the name suggest, Depth First Search starts searching or traversing the tree from the root and it goes down to the depth of the tree, Hence Depth-first search. Once it reaches the last node in depth, the algorithm backtracks mean it starts traveling backward until it reaches the root of the tree again. The algorithm then starts scanning the other part of the tree.

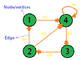
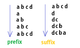
Figure 1.1

Figure 1.2

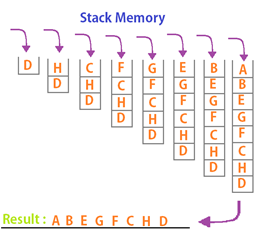
In figure 1.1, We have a graph let us say, Graph G. Figure 1.2 shows us exactly how the algorithm traverse the graph and internally store all the nodes it has visited. In Figure 1.2, we can see that a computer memory called Stack memory is used to keep track of all the nodes the algorithm have visited. As it keeps traversing through the dept of the graph it stores all the nodes in the stack memory. Later on, when the graph is completely traced and all the nodes are stored in the stack memory, The computer then uses that stack memory and prints all the nodes that is has visited. The stack works as a LIFO ( Last In First Out). Finally, When all the nodes are pushed in the LIFO manner, It is popped the same(LIFO) manner. As we can see in figure 1.2, the result is all the node that are stored in the stack from top to bottom.

Example 2: Graph G3. Figure 2:

Figure 2.1

Figure 2.2

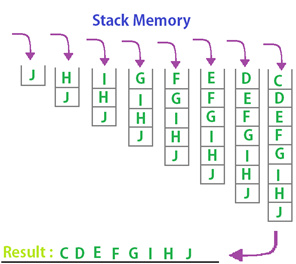
Figure 2 represents another example of Depth First Search algorithm.

Breadth First Search:

This is another search algorithm that is used for tree or graph data structure. Much like Depth First Search this algorithm Searches the graphs but with respect to the graph's Breadth. In other words, BFS follows breadth ward motion for traversing the graph or tree for that matter. Contrary to Depth first search this algorithm scans the breadth first and then goes not to the depth of the tree. For storing information, Breadth First search uses Queue data structure rather than Stack data structure which is used by DFS.

A queue is an abstract data type that uses FIFO system whereas stack uses LIFO system. FIFO stands for First In First Out, meaning the data that enters first in the queue is popped first from the queue. The case is opposite with the LIFO system, where the data that entered first is popped last out of the stack.

Let us take an example to understand the BFS better:

Example 1: BFS on Figure 3.

Figure 3.1: Graph G4.

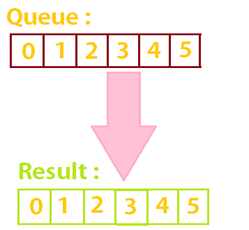
Figure 3.2: Queue.

From figure 3.2, we can easily make out that Breadth First Search uses Queue to store information on the nodes that has been traversed. Also, since queue uses First In First Out system, the sequence is the same in the queue and in the final result.

Example 2: BFS on Directed Graph 4.

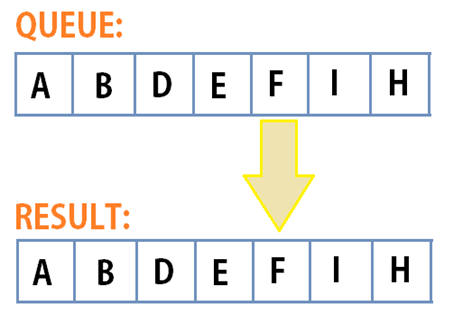
Figure 4.1: Directed Graph.

Figure 4.2: Queue.

Example 3: BFS on Directed Graph G5.

Figure 5.1: Directed Graph.

Figure 5.2 : Queue Representation.

Linked List:

Linked list is yet another data structure that is used to store information much like Queues, stacks, and arrays. Linked list is much similar to arrays in the sense that they are connected together. In the case of Linked list, all the elements are connected with links. Linked list can be used to represent graphs and trees. Each node can store information like the name of the node and also the address to its next node or child node. Arrays are static data structure meaning they that arrays cannot expand will the program is being executed. Whereas, Linked list is a dynamic data structure which provides linked list an edge over arrays. Linked list are very commonly used since it provides full access to memory allocation to the programmer.

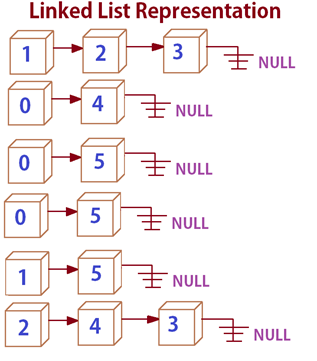
Representation of a graph in Linked list :

Figure 6.1: Graph

Figure 6.2: Linked List representation.

Prim's Algorithm:

Prim's Algorithm is a pathfinding algorithm. Usually, Prim's Algorithm is used for finding shortest path in a graph or a tree. Prim's Algorithm is also called Prim's spanning tree or Minimum spanning tree. Basically, This algorithm finds the shortest path available from point A to point B.

In a real world application, Prim's algorithm is used in Navigation applications such Google maps. As we know Google maps give us information like how much duration the travel takes by car, bus, train or plane. The ability to figure out how many alternative route we have from source to destination and which one is the shortest, Comes from this powerful Prim's algorithm.

Here is the Prim's Algorithm:

1. 1
   Remove all the Loops and parallel edges in a graph.

   Advertisement

   Was this step helpful? Yes | No| I need help
2. 2
   Choose any random node as source

   .

   Was this step helpful? Yes | No| I need help
3. 3
   Check all the outgoing edges.

   Was this step helpful? Yes | No| I need help
4. 4
   Find the one edges with the lowest cost.

   Was this step helpful? Yes | No| I need help
5. 5
   Repeat until all the nodes are visited.

   Was this step helpful? Yes | No| I need help

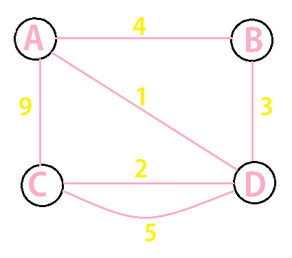
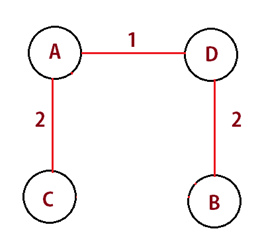
Let us take an example now. Example : Identify the shortest path.

Step 1 : Remove all the loops from the graph, i.e Node A and Node C (Figure 7.1).

Figure 7.1

Step 2 : Remove all parallel edges from the graph, i.e Path (D >> C) (Figure 7.2).

Figure 7.2

Step 3 : Make a Graph Matrix (Figure 7.3).

Figure 7.3

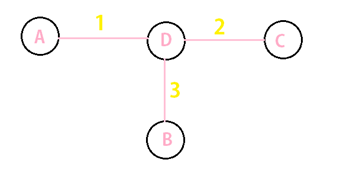
Step 4 : Check the minimum weight according to the row and make the vertices (Figure 7.4).

Figure 7.4

Hence the Minimum Spanning Tree. Now, To calculate the total weight of this tree:

Total weight = 1 + 2 + 3 = 6 Therefore, The total weight of the tree is 6.

Formulae :

• To find edges : (n-1) where n is the number of nodes.

• To find Total Vertices : (n) where n is the number of nodes.

Kruskal's Algorithm:

Kruskal's Algorithm is yet another minimum cost spanning tree. It is similar to Prim's Algorithm but follows a bit different approach. In Kruskal's algorithm we use Greedy approach. This algorithm treats every graph as a forest and every node as a tree in that forest.

Here is the Kruskal's algorithm:

Remove all loops and parallel edges from the graph. Arrange all the edges in the increasing order of weight. Add the edge with the least weight. Repeat until all the nodes are visited.

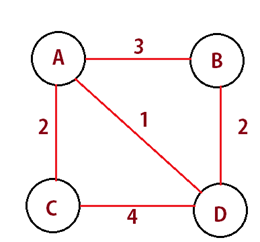
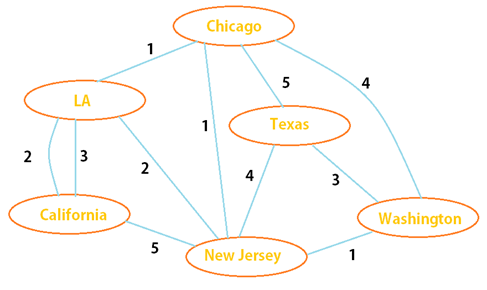
Example:

Figure 8.1

Step 1: Remove all loops and parallel edges (Figure 8.2).

Figure 8.2

Step 2: Create Edge table (Figure 8.3).

Figure 8.3

Step 3: Add the edges with the least weight (Figure 8.4).

Figure 8.4

Total weight = (2 + 1 + 2) = 5

Hence, total weight of the graph is 5.

Total Vertices = n -1 = 4 - 1 = 3 Hence, total vertices is 3.

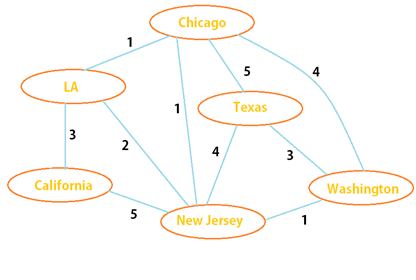
Example :

Figure 9.1

Step 1: Remove all the loops and Parallel edges from the graph (Figure 9.2).

Figure 9.2

Step 2 : Create Edge table (Figure 9.3).

Figure 9.3

Step 3: Add edges with the lowest weight (Figure 9.4).

Figure 9.4 Example :

Figure 10.1

Step 1 : Remove all the loops and parallel edges from the graph (Figure 10.2).

Figure 10.2

Step 2 : Create edge table of the graph (Figure 10.3).

Figure 10.3

Total weight of the graph :

Total weight = ( 1 + 2 + 5 + 1 + 4 + 3 + 5 + 1 + 2 + 4) = 28

Hence, Total weight of the graph is 28.

Dijkstra's algorithm:

Dijkstra's algorithm is shortest path finding algorithm similar to Prim's and Kruskal's Algorithm. Dijkstra's algorithm was invented by computer scientist Edsger Dijkstra in 1959. Dijkstra's algorithm finds the shortest path in a given graph between nodes which are connected in a network. In Dijkstra's algorithm, we travel on minimum edge or path only.

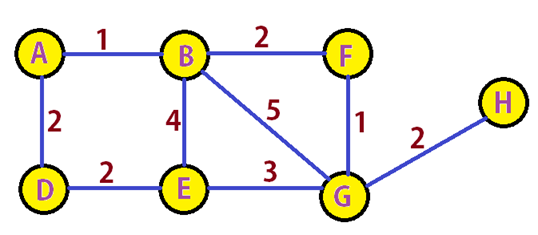
Now, Let's consider an example to understand Dijkstra's algorithm better. Example: Find Shortest path using Dijkstra's algorithm.

Figure 11.0

Figure 11.1: Double Cost.

Shortest path = (1 + 2 + 1 + 4 + 2 + 2) = (12)

Hence, The shortest path of the graph 11.0 is 12.

Example 2: Find the shortest path using Dijkstra's algorithm.

Figure 12.0: Graph.

Figure 12.1: Shortest path.

Total weight of the Graph 12:

Total weight = ( 2 + 1 + 5 + 2 + 3) = (13)

Hence, The total weight of the Graph 12 with the shortest path is 13.

1) Design and Algorithm Analysis Overview

2) Algorithm Analysis

3) Algorithm Sorting

4) Algorithm Graph in Data Structure

5) Algorithm_Search

6) Types of Algorithm Laws

7) Design and Algorythm of Dynamic Programming

If you need to reference this article in your work, you can copy-paste the following depending on your required format:

APA (American Psychological Association)
Types and Styles of Algorithm Searchs. (2017). In ScienceAid. Retrieved Jun 4, 2023, from https://scienceaid.net/Algorithm_Search

MLA (Modern Language Association) "Types and Styles of Algorithm Searchs." ScienceAid, scienceaid.net/Algorithm_Search Accessed 4 Jun 2023.

Chicago / Turabian ScienceAid.net. "Types and Styles of Algorithm Searchs." Accessed Jun 4, 2023. https://scienceaid.net/Algorithm_Search.

If you have problems with any of the steps in this article, please ask a question for more help, or post in the comments section below.

Comments